Coretan Kehidupan: BAB 3, DISTRIBUSI FREKUENSI DAN GRAFIK

Suatu tabel yang menyajikan kelas-kelas data beserta frekuensinya disebut distribusi frekuensi atau tabel frekuensi.

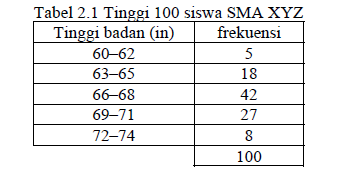
CONTOH: Berikut distibusi frekuensi tinggi badan 100 siswa SMA XYZ

Berdasarkan tabel di atas, banyak siswa yang tingginya berada dalam rentang 66 in dan 68 in adalah 42 orang. Salah satu kelemahan penyajian data dalam tabel frekuensi adalah tidak terlihatnya data asli atau data mentahnya.

Beberapa istilah pada tabel frekuensi

INTERVAL KELAS adalah interval yang diberikan untuk menetapkan kelas-kelas dalam distribusi. Pada tabel 2.1, interval kelasnya adalah 60-62, 63-65, 66-68, 69-71 dan 72-74. Interval kelas 66-68 secara matematis merupakan interval tertutup [66, 68], ia memuat semua bilangan dari 66 sampai dengan 68. Bilangan 60 dan 62 pada interval 60-62 disebut limit kelas, dimana angka 60 disebut limit kelas bawah dan angka 62 disebut limit kelas atas.

BATAS KELAS adalah bilangan terkecil dan terbesar sesungguhnya yang masuk dalam 60 – 62. Bilangan 59.5 dan 62.5 ini disebut batas kelas atau limit kelas sesungguhnya, kelas interval tertentu. Misalnya jika dalam pengukuran tinggi badan di atas dilakukan dengan ketelitian 0.5 in maka tinggi badan 59.5 in dan 62.5 in dimasukkan ke dalam kelas dimana bilangan 59.5 disebut batas kelas bawah dan 62.5 disebut batas kelas atas. Pada prakteknya batas kelas interval ini ditentukan berdasarkan rata-rata limit kelas atas suatu interval kelas dan limit kelas bawah interval kelas berikutnya. Misalnya batas kelas 62.5 diperoleh dari (62+63)/2. Pemahaman yang sama untuk interval kelas lainnya.

LEBAR/PANJANG INTERVAL KELAS adalah selisih antara batas atas dan batas bawah batas kelas. Misalnya lebar intervl kelas 60-62 adalah 62.5–59.5 = 3

TANDA KELAS adalah titik tengah interval kelas. Ia diperoleh dengan cara membagi dua jumlah dari limit bawah dan limit atas suatu interval kelas. Contoh tanda kelas untuk kelas interval 66-68 adalah (66+68)/2 = 67.

Prosedur umum membuat tabel frekuensi

Tetapkan data terbesar dan data terkecil, kemudian tentukan rangenya.
Bagilah range ini ke dalam sejumlah interval kelas yang mempunyai ukuran sama. Jika tidak mungkin, gunakan interval kelas dengan ukuran berbeda. Biasanya banyak interval kelas yang digunakan antara 5 dan 20, bergantung pada data mentahnya. Diupayakan agar tanda kelas merupakan data observasisesungguhnya. Hal ini untuk mengurangi apa yang disebut dengan groupingerror. Namun batas kelas sebaiknya tidak sama dengan data observasi. Dapat menggunakan rumus: k=1+3,3 log n, dimana k adalah banyaknya kelas dan n adalah jumlah data
Hitung lebar interval kelas, lalu hasilnya dibulatkan. Lebar Interval (d) = Range:Banyak interval kelas
Starting point: mulailah dengan bilangan limit bawah untuk kelas interval pertama. Dapat dipilih sebagai data terkecil dari observasi atau bilangan di bawahnya.
Dengan menggunakan limit bawah interval kelas pertama dan lebar interval kelas, tentukan limit bawah interval kelas lainnya.
Susunlah semua limit bawah interval kelas secara vertikal, kemudian tentukan limit atas yang bersesuaian. Kembalilah ke data mentah dan gunakan turus untuk memasukkan data pada interval kelas yang ada.

CONTOH: Berikut nilai 80 siswa pada ujian akhir mata pelajaran matematika:

Langkah-langkah untuk membuat tabel distribusi frekuensi dilakukan sebagai berikut:

Nilai tertinggi = 97 dan nilai terendah 53. Jadi range = 97-53 = 44.
Tetapkan jumlah kelas; dalam hal ini diambil 10.
Lebar interval kelas d = 44/10 = 4.4 dibulatkan menjadi 5.
Diambil bilangan 50 sebagai limit bawah untuk kelas pertama.
Limit atas kelas interval yang bersesuaian adalah 54 untuk kelas pertama, 59 untuk kelas kedua, dan seterusnya.
Selanjutnya, limit bawah untuk kelas kedua adalah 50+5 = 55, limit bawah kelas ketiga 55+5 = 60 dan seterusnya. Gunakan turus untuk memasukkan data ke dalam interval kelas

Hasilnya seperti terlihat pada Tabel 2.3 berikut:

Akhirnya diperoleh tabel distribusi frekuensi sebagai berikut:

Melalui tabel ini kita dapat mengetahui pola penyebaran nilai siswa. Paling banyak nilai siswa mengumpul pada interval 75-79, paling sedikit data termuat dalam interval 50-54. Sedangkan siswa yang mendapat nilai istimewa atau di atas 90 hanya ada 8 orang.

- Tabel Distribusi Frekuensi Relatif

Nilai frekuensinya TIDAK dinyatakan dalam bentuk ANGKA MUTLAK, tapi dalam bentuk ANGKA PERSENTASE (%) atau ANGKA RELATIF.

Rumus mencari frekuensi relatif adalah :

Contoh:

(Menggunakan soal dan tabel distribusi frekuensi MUTLAK)

Maka, untuk membuat tabel distribusi frekuensi relatif (%) adalah dengan mencari frekuensi relatif (%) untuk setiap interval kelasnya dulu.
Jawab :
f relatif kelas ke-1 = 1/40 x 100%    = 2,5%
f relatif kelas ke-2 = 2/40 x 100%    = 5%
f relatif kelas ke-3 = 17/40 x 100% = 42,5%
f relatif kelas ke-4 = 3/40 x 100%    = 7,5%
f relatif kelas ke-5 = 10/40 x 100% = 25%
f relatif kelas ke-6 = 7/40 x 100%    = 17,5% +
Total    = 100%

Lalu masukkan hasil perhitungan frekuensi relatif tersebut ke dalam tabel.

-DISTRIBUSI FREKUENSI KUMULATIF
Distribusi Frekuensi Kumulatif (fkum ) adalah distribusi yang nilai frekuensinya (f) diperoleh dengan cara MENJUMLAHKAN frekuensi demi frekuensi.
Distribusi Frekuensi Kumulatif terbagi menjadi 2, yaitu :
- Distribusi Frekuensi Kumulatif “KURANG DARI”
- Distribusi Frekuensi Kumulatif “ATAU LEBIH”

Contoh (mengacu pada frekuensi mutlak di atas).

Dengan mengacu pada tabel Distribusi Frekuensi Mutlak di atas, maka contoh Tabel Distribusi Frekuensi Kumulatif nya :

Keterangan Tabel Distribusi Frekuensi Kumulatif “KURANG DARI” :

Untuk acuan penentuan nilai, menggunakan nilai ujung bawah kelas.

Penentuan frekuensi kumulatif melihat dari frekuensi pada tabel distribusi frekuensi (mutlak) lalu dikumulasikan sesuai dengan kategori nilai pada tabel distribusi frekuensi kumulatif.

Ada penambahan 1 kelas, yaitu “KURANG DARI 87” dikarenakan nilai data terbesar adalah 85, sehingga kalau nilai “KURANG DARI” hanya sampai ke “KURANG DARI 80” saja, maka untuk data nilai yang LEBIH DARI 80 tidak masuk hitungan padahal ada frekuensinya.

Sedangkan untuk Distribusi Frekuensi Kumulatif “ATAU LEBIH”, contohnya adalah :

Keterangan Tabel Distribusi Frekuensi Kumulatif “ATAU LEBIH”

Konsep perhitungan frekuensi kumulatifnya sama dengan frekuensi kumulatif “KURANG DARI”, hanya saja kalau tabel distribusi frekuensi kumulatif “ATAU LEBIH” mengacu pada nilai “ATAU LEBIH” nya, sehingga kita tinggal mencari berapa frekuensi kumulatifnya dengan melihat dari frekuensi (mutlak).

-DISTRIBUSI FREKUENSI KUMULATIF RELATIF

Distribusi Frekuensi Kumulatif Relatif {fkum (%)} adalah distribusi frekuensi yang NILAI FREKUENSI KUMULATIF diubah menjadi NILAI FREKUENSI RELATIF atau dalam bentuk persentase (%).
Distribusi Frekuensi Kumulatif Relatif juga terbagi menjadi :

Distribusi Frekuensi Kumulatif Relatif “KURANG DARI”

Distribusi Frekuensi Kumulatif Relatif “ATAU LEBIH”

Konsep Distribusi Frekuensi Kumulatif Relatif adalah :

TIDAK menggunakan angka mutlak, jadi menggunakan persentase.

Mengambil frekuensinya dari tabel DISTRIBUSI FREKUENSI KUMULATIF.

Rumus untuk mencari Frekuensi Kumulatif Relatif (%) adalah :

Dengan mengacu pada tabel distribusi frekuensi kumulatif “KURANG DARI” di atas, maka perhitungan frekuensi kumulatif relatifnya adalah :
F kum (%) kelas ke-1 = 0/40 x 100% = 0 %
F kum (%) kelas ke-2 = 1/40 x 100% = 2,5%
F kum (%) kelas ke-3 = 3/40 x 100% = 7,5%
F kum (%) kelas ke-4 = 20/40 x 100% = 50%
F kum (%) kelas ke-5 = 23/40 x 100% = 57,5%
F kum (%) kelas ke-6 = 33/40 x 100% = 82,5%
F kum (%) kelas ke-7 = 40/40 x 100% = 100%
Dari perhitungan di atas lalu dimasukkan ke dalam tabel.

Untuk Distribusi Frekuensi Kumulatif Relatif “ATAU LEBIH” juga sama rumus perhitungannya.

Dari tabel distribusi frekuensi kumulatif “ATAU LEBIH” di atas, bisa dilakukan perhitungan untuk mencari Frekuensi Kumulatif Relatif “ATAU LEBIH” :
F kum (%) kelas ke-1 = 40/40 x 100% = 100%
F kum (%) kelas ke-2 = 39/40 x 100% = 97,5 %

F kum (%) kelas ke-3 = 37/40 x 100% = 92,5 %
F kum (%) kelas ke-4 = 20/40 x 100% = 50%
F kum (%) kelas ke-5 = 17/40 x 100% = 42,5 %
F kum (%) kelas ke-6 = 7/40 x 100% =7,5 %
F kum (%) kelas ke-7 = 0/40 x 100% = 0%

Setelah selesai melakukan perhitungan, lalu masukkan hasilnya ke dalam tabel distribusi frekuensi kumulatif relatif “ATAU LEBIH”.

Grafik merupakan lukisan pasang surutnya suatu keadaan dengan garis atau gambar atau dengan kata lain, Grafik menggambarkan naik atau turunnya hasil statistik.

Dengan masih mengacu pada Tabel Distribusi Frekuensi, maka bisa digambarkan dengan cara membuat grafik :
- Histogram
- Poligon Frekuensi
- Ogive

HISTOGRAM

-Histogram merupakan grafik yang menggambarkan suatu distribusi frekuensi dengan bentuk beberapa segiempat atau menyerupai diagram batang.

-Langkah-langkah membuat Histogram :

Buat “absis” dan “ordinat” . absis adalah sumbu mendatar atau sumbu X yang menyatakan NILAI; ordinat adalah sumbu tegak atau sumbu Y yang menyatakan FREKUENSI.

Buat skala absis dan skala ordinatnya dengan melihat dari nilai dan frekuensinya.

Buat Batas Kelas

Batas Kelas :
Batas kelas ke-1 : 45 – 0,5 = 44,5
Batas kelas ke-2 : ( 51 + 52) x ½ = 51,5
Batas kelas ke-3 : (58 + 59) x ½ = 58,5
Batas kelas ke-4 : (65+66) x ½ = 65,5
Batas kelas ke-5 : (72+73) x ½ = 72,5
Batas kelas ke-6 : (79+80) x ½ = 79,5
Batas kelas ke-7 : 86 + 0,5 = 86,5
Lalu masukkan ke dalam tabel dan sesuaikan dengan frekuensinya.

POLIGON FREKUENSI

- Poligon Frekuensi merupakan grafik garis yang menghubungkan NILAI TENGAH tiap sisi atas yang berdekatan dengan NILAI TENGAH jarak frekuensi mutlak masing-masing.

-Perbedaan antara HISTOGRAM dengan POLIGON FREKUENSI adalah :

Histogram menggunakan BATAS KELAS ; sedangkan POLIGON menggunakan TITIK TENGAH.

Grafik HISTOGRAM berwujud SEGIEMPAT atau menyerupai DIAGRAM BATANG; sedangkan POLIGON berwujud GARIS atau KURVA yang saling berhubungan satu sama lain.

-Langkah-langkah membuat POLIGON FREKUENSI :

Buat TITIK TENGAH kelas dengan cara : (NILAI UJUNG BAWAH KELAS + NILAI UJUNG ATAS KELAS) x ½

Buat TABEL DISTRIBUSI FREKUENSI yang MUTLAK disertai dengan kolom tambahan berupa kolom TITIK TENGAH KELAS tsb.

Buat grafik poligon frekuensi dengan melihat data pada tabel distribusi frekuensi mutlak

a. Buat TITIK TENGAH KELAS
Titik tengah kelas ke-1 : (45 + 51) x ½ = 48
Titik tengah kelas ke-2 : (52 + 58) x ½ = 55
Titik tengah kelas ke-3 : (59 + 65) x ½ = 62
Titik tengah kelas ke-4 : (66 + 72) x ½ = 69
Titik tengah kelas ke-5 : (73 + 79) x ½ = 76
Titik tengah kelas ke-6 : (80 + 86) x ½ = 83

b. Buat Tabel Distribusi Frekuensi Mutlak dengan menambah kolom TITIK TENGAH KELAS

c. Buat grafik poligon frekuensi

OGIVE

-Ogive biasanya digunakan untuk sensus penduduk tentang perkembangan kelahiran dan kematian bayi, perkembangan penjualan suatu produk, perkembangan dan penjualan saham, dsb.
Contoh Penerapan Grafik Ogive
1. Grafik Ogive berdasarkan dari Tabel Distribusi Frekuensi Kumulatif “KURANG DARI” dan Tabel Distribusi Frekuensi Kumulatif “ATAU LEBIH”.